しんごのキになる話⑨　すごい植物たちの巻（フィボナッチ数列　その２）

この数列を「フィボナッチ数列」と言い、動物や植物たちの成長に応用されているのです。

植物でいえば例えば花びらの数です。花びらは三枚から始まるものが多いですよね。

そしてその他の花びらの数も大体決まっているのです。

ユリ	サクラ	コスモス	マリーゴールド	マーガレット	デージー	ガーベラ
3枚	5枚	8枚	13枚	21枚	34枚	55枚

私が朝の散歩で見かける草花の花びらも5枚が多いのです。

しかし、花びらが4枚、7枚、11枚、18枚の草花もあります。

これらはフィボナッチ数列から外れています。これらもある数列に従っているのです。

それは、フィボナッチ数列の最初の数字の１を２に変えると規則性が出来るのです。

２、１、３、４、７、１１、１８、２９、、、、、となるのです。

これはリュカ数列と呼ばれる数列です。

そして、茎につく葉の位置もフィボナッチ数列に沿っているのです。

葉は植物が生きて行くための栄養をつくる光合成をおこないます。そのために光がより多く当たるように葉の位置を少しずつ変えていきます。その葉のつき方は「葉序」と呼ばれます。

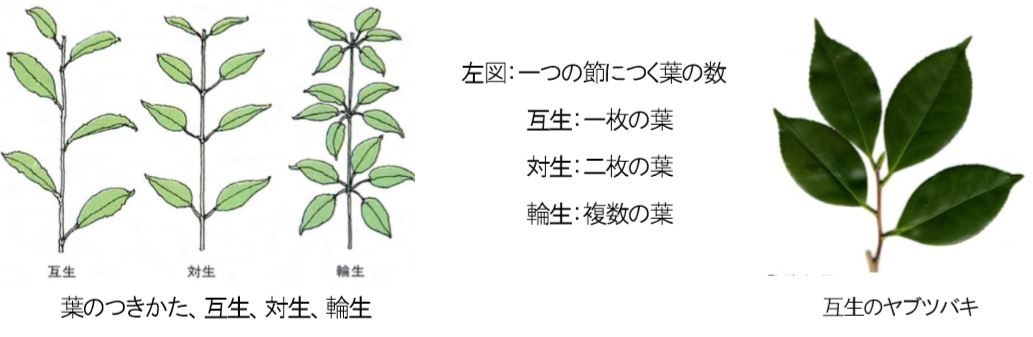
対生は茎の一つの節から二枚の葉が向かい合って出る形式です。

そして次の節で90度回転してまた一対の対生の葉がつけば、上から見ると十字架に見えます。

でも、これは別に「ダ・ビンチ・コード」の続きではありません。

（フィボナッチ数列の項　その３　へ続く）